viernes, 15 de junio de 2012

ESTADISTICA NO PARAMÉTRICA

La estadística no paramétrica es una rama de la estadística que estudia las pruebas y modelos estadísticos cuya distribución subyacente no se ajusta a los llamados criterios paramétricos.

Su distribución no puede ser definida a priori, pues son los datos observados los que la determinan.

La utilización de estos métodos se hace recomendable cuando no se puede asumir que los datos se ajusten a una distribución conocida, cuando el nivel de medida empleado no sea, como mínimo, de intervalo.

Las principales pruebas no paramétricas son las siguientes:

Prueba χ² de Pearson
Prueba binomial
Prueba de Anderson-Darling
Prueba de Cochran
Prueba de Cohen kappa
Prueba de Fisher
Prueba de Friedman
Prueba de Kendall
Prueba de Kolmogórov-Smirnov
Prueba de Kruskal-Wallis
Prueba de Kuiper
Prueba de Mann-Whitney o prueba de Wilcoxon
Prueba de McNemar
Prueba de la mediana
Prueba de Siegel-Tukey
Coeficiente de correlación de Spearman
Tablas de contingencia
Prueba de Wald-Wolfowitz
Prueba de los signos de Wilcoxon

La mayoría de estos test estadísticos están programados en los paquetes estadísticos más frecuentes, quedando para el investigador, simplemente, la tarea de decidir por cuál de todos ellos guiarse o qué hacer en caso de que dos test nos den resultados opuestos

Hay que decir que, para poder aplicar cada uno existen diversas hipótesis nulas que deben cumplir nuestros datos para que los resultados de aplicar el test sean fiables.

Esto es, no se puede aplicar todos los test y quedarse con el que mejor convenga para la investigación sin verificar si se cumplen las hipótesis necesarias.

La violación de las hipótesis necesarias para un test invalidan cualquier resultado posterior y son una de las causas más frecuentes de que un estudio sea estadísticamente incorrecto.

Esto ocurre sobre todo cuando el investigador desconoce la naturaleza interna de los test y se limita a aplicarlos sistemáticamente.

Prueba de los signos de Wilcoxon

La prueba de los signos de Wilcoxon es una prueba no paramétrica para comparar la mediana de dos muestras relacionadas y determinar si existen diferencias entre ellas. Se utiliza como alternativa a la prueba t de Student cuando no se puede suponer la normalidad de dichas muestras.

Debe su nombre a Frank Wilcoxon, que la publicó en 1945. Se utiliza cuando la variable subyacente es continua pero presupone ningún tipo de distribución particular.

Planteamiento

Supóngase que se dispone de n pares de observaciones, denominadas $(x_i, y_i)$ . El objetivo del test es comprobar si puede dictaminarse que los valores $x_i$ e $y_i$ son o no iguales.

Suposiciones

Si $z_i=y_i-x_i$ , entonces los valores $z_i$ son independientes.

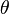Los valores $z_i$ tienen una misma distribución continua y simétrica respecto a una mediana común $\theta$ .

Método

La hipótesis nula es $H_0$ : $\theta=0$ . Retrotrayendo dicha hipótesis a los valores $x_i, y_i$ originales, ésta vendría a decir que son en cierto sentido del mismo tamaño.

Para verificar la hipótesis, en primer lugar, se ordenan los valores absolutos $|z_1|,\dots,|z_n|$ y se les asigna su rango $R_i$ . Entonces, el estadístico de la prueba de los signos de Wilcoxon, $W^+$ , es

$W^+=\sum_{z_i > 0} R_i,$

es decir, la suma de los rangos $R_i$ correspondientes a los valores positivos de $z_i$ .

La distribución del estadístico $W^+$ puede consultarse en tablas para determinar si se acepta o no la hipótesis nula.

En ocasones, esta prueba se usa para comparar las diferencias entre dos muestras de datos tomados antes y después del tratamiento, cuyo valor central se espera que sea cero.

Las diferencias iguales a cero son eliminadas y el valor absoluto de las desviaciones con respecto al valor central son ordenadas de menor a mayor.

A los datos idénticos se les asigna el lugar medio en la serie. la suma de los rangos se hace por separado para los signos positivos y los negativos. S representa la menor de esas dos sumas.

Comparamos S con el valor proporcionado por las tablas estadísticas al efecto para determinar si rechazamos o no la hipótesis nula, según el nivel de significación elegido.

Prueba U de Mann-Whitney

La prueba U de Mann-Whitney (también llamada de Mann-Whitney-Wilcoxon, prueba de suma de rangos Wilcoxon, o prueba de Wilcoxon-Mann-Whitney) es una prueba no paramétrica aplicada a dos muestras independientes.

Es, de hecho, la versión no paramétrica de la habitual prueba t de Student.

Fue propuesto inicialmente en 1945 por Frank Wilcoxon para muestras de igual tamaños y extendido a muestras de tamaño arbitrario como en otros sentidos por Henry B. Mann y D. R. Whitney en 1947.

Planteamiento de la prueba

La prueba de Mann-Whitney se usa para comprobar la heterogeneidad de dos muestras ordinales. El planteamiento de partida es:

Las observaciones de ambos grupos son independientes
Las observaciones son variables ordinales o continuas.
Bajo la hipótesis nula, las distribuciones de partida de ambas distribuciones es la misma
Bajo la hipótesis alternativa, los valores de una de las muestras tienden a exceder a los de la otra: P(X > Y) + 0.5 P(X = Y) > 0.5.

Cálculo del estadístico

Para calcular el estadístico U se asigna a cada uno de los valores de las dos muestras su rango para construir

$U_1=R_1 - {n_1(n_1+1) \over 2}$

$U_2=R_2 - {n_2(n_2+1) \over 2}$

donde n₁ y n₂ son los tamaños respectivos de cada muestra; R₁ y R₂ es la suma de los rangos de las observaciones de las muestras 1 y 2 respectivamente.

El estadístico U se define como el mínimo de U₁ y U₂.

Los cálculos tienen que tener en cuenta la presencia de observaciones idénticas a la hora de ordenarlas. No obstante, si su número es pequeño, se puede ignorar esa circunstancia.

Distribución del estadístico

La prueba calcula el llamado estadístico U, cuya distribución para muestras con más de 20 observaciones se aproxima bastante bien a la distribución normal.

La aproximación a la normal, z, cuando tenemos muestras lo suficientemente grandes viene dada por la expresión:

$z=(U-m_U)/\sigma_{U}$

Donde m_U y σ_U son la media y la desviación estándar de U si la hipótesis nula es cierta, y vienen dadas por las siguientes fórmulas:

$m_U=n_1 n_2/2.$

$\sigma_U=\sqrt{n_1 n_2 (n_1+n_2+1) \over 12}.$

Implementaciones

Implementación en línea usando javascript
R tiene una implementación del test (al que se refiere como el Wilcoxon two-sample test) mediante wilcox.test (y para el caso de datos pareados, wilcox.exact en el paquete exactRankTests o con la opción exact=FALSE).

Prueba De Rachas

sirve para detectar aleatoriedad, que se basa en el número de series o rachas que hay en una secuencia de datos.

La prueba aplica sólo si podemos asignar a cada uno de los valores de los datos a una de dos categorías distintas.

La prueba de rachas de una sola muestra nos permite determinar si el número de rachas en una muestra de datos, es o no suficientemente pequeño o suficientemente grande para rechazar la hipótesis nula de que la secuencia observada se debe al azar.

Definimos una racha como una secuencia de datos semejantes precedidas y seguidas por un tipo diferente de observación o por ninguna observación

Ejemplo:

1. Supongamos, por ejemplo, que un lunes por la mañana se presentan cierto número de hombres y de mujeres a la oficina de transito para pedir licencias de conducir en el siguiente orden

MM H MM H MM HH M HHH MMMM

En esta secuencia hay un total de nueve rachas. Tenemos una racha que consta de dos mujeres, seguida de una de un hombre, seguida de otra de dos mujeres, etc.

Prueba de la mediana

La prueba de la mediana es una prueba no paramétrica que podemos considerar un caso especial de la prueba de chi-cuadrado, pues se basa en esta última.

Su objetivo es comparar las medianas de dos muestras y determinar si pertencen a la misma población o no.

Para ello, se calcula la mediana de todos los datos conjuntamente. Después, se divide cada muestra en dos subgrupos: uno para aquellos datos que se sitúen por encima de la mediana y otro para los que se sitúen por debajo.

La prueba de chi-cuadrado determinará si las frecuencias observadas en cada grupo difieren de las esperadas con respecto a una distribución de frecuencias que combine ambas muestras.

Esta prueba está especialmente indicada cuando los datos sean extremos o estén sesgados.

PRUEBA BINOMIAL

La prueba binomial analiza variables dicotómicas y compara las frecuencias observadas en cada categoría con las que cabría esperar según una distribución binomial de parámetro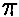

especificado en la hipótesis nula tal como se ha explicado en elcapítulo anterior *.

La secuencia para realizar este contraste es:

Analizar

Pruebas no paramétricas

Binomial

Escalas de medición

Escalas de medición son una sucesión de medidas que permiten organizar datos en orden jerárquico. Las escalas de medición, pueden ser clasificadas de acuerdo a una degradación de las características de las variables.

Estas escalas son: nominales, ordinales, intervalares o racionales. Según pasa de una escala a otra el atributo o la cualidad aumenta.

Las escalas de medición ofrecen información sobre la clasificación de variables discretas o continuas, tambien mas conocidas como escalas grandes o pequeñas. Toda vez que dicha clasificación determina la selección de la gráfica adecuada.

Niveles de clasificación

La medición puede definirse como la asignación de numerales a objetos o sucesos siguiendo ciertas reglas Stevens (1946).

El autor de esta definición desarrolló un método para clasificar los diferentes resultados de las mediciones en lo que llamó niveles de medición.

Un nivel de medición es la escala que representa una jerarquía de precisión dentro de la cual una variable puede evaluarse, en función de las características que rigen las escalas.

Por ejemplo, la variable estatura puede analizarse en diferentes niveles de medida.

Un conjunto de personas pueden clasificarse en altos y bajos, A y B respectivamente, creando dos grupos.

Para ello no es necesario recurrir a ninguna cinta métrica, simplemente basta observar quienes destacan sobre los demás (el grupo de altos) y el resto completarán el grupo de bajos.

El nivel de medición que corresponde a esta forma de medir es nominal.

También podrían alinearse a los sujetos y ordenarlos según su altura, el primero sería el más alto y el último el más bajo, el resto se organizaría de forma que cada persona tuviese delante a uno más alto y detrás a uno más bajo.

El nivel de medición en este caso es ordinal. Hasta el momento no es posible decir cuánto es una persona más alta que otra.

A través del número de personas que hay entre dos sujetos, por ejemplo, Andréa y Juan en la fila ordenada anteriormente.

En este caso además del orden se conoce la magnitud de la altura. Si en lugar de utilizar el número de personas se recurre a una regla se puede ofrecer otra medida de la altura. Esta forma de medir es propia del nivel de intervalos, que permite saber la magnitud de los elementos comparando unos con otros.

La cuarta posibilidad es utilizar un metro que sitúa el cero en el mismo suelo y, por lo tanto, la altura se define en función de la distancia desde la cabeza al suelo (valor cero absoluto donde se sitúa la ausencia de altura).

En ciencias sociales es poco frecuente encontrar variables en niveles de razón, normalmente son nominales, ordinales y en ocasiones de intervalos, rara vez de razón. Una característica de esta clasificación es que las propiedades de una escala se cumplen en el nivel superior.

En la estadística descriptiva y con el fin de realizar pruebas de significancia, las variables se clasifican de la siguiente manera de acuerdo con su nivel de medida:

nominal (también categórica o discreta)
ordinal
de intervalo o intervalar (continua)
de razón o racional (continua)

Las variables de intervalo y de razón también están agrupadas como variables continuas.

Medida nominal

El nivel nominal de medición, de la palabra latina nomún (nombre) describe variables de naturaleza categórica que difieren en calidad más que en cantidad (Salkind, 1998: 113).

Ante las observaciones que se realizan de la realidad, es posible asignar cada una de ellas exclusivamente a una categoría o grupo. Cada grupo o categoría se denomina con un nombre o número de forma arbitraria, es decir, que se etiqueta en función de los deseos o conveniencia del investigador.
Este nivel de medición es exclusivamente cualitativo y sus variables son por lo tanto cualitativas.

Por ejemplo, los sujetos que son del curso de A de 2º de eso y los de B generan dos grupos. Cada sujeto se asigna a un grupo, y las variables son de tipo cualitativo (de calidad) y no cuantitativo puesto que indica donde está cada sujeto y no "cuanto es de un curso y no de otro". En este ejemplo los números 2 y 3 pueden sustituir las letras A y B, de forma que 2 y 3 son simples etiquetas que no ofrecen una valoración numérica sino que actúan como nominativos.

En esta escala hay que tener en cuenta dos condiciones:

No es posible que un mismo valor o sujeto esté en dos grupos a la vez. No se puede ser de 2º y 3º a la vez. Por lo tanto este nivel exige que las categorías sean mutuamente excluyentes entre sí.
Los números no tienen valor más que como nombres o etiquetas de los grupos.

En este tipo de medidas, se asignan nombres o etiquetas a los objetos. La asignación se lleva a cabo evaluando, de acuerdo con un procedimiento, la similaridad de la instancia a ser medida con cada conjunto de ejemplares nominados o definiciones de categorías.

El nombre de la mayoría de los ejemplares nominados o definiciones es el “valor” asignado a la medida nominal de la instancia dada. Si dos instancias tienen el mismo nombre asociado a ellas, entonces pertenecen a la misma categoría, y ese es el único significado que las medidas nominales tienen.

Esta escala comprende variables categóricas que se identifican por atributos o cualidades. Las variables de este tipo nombran e identifican distintas categorías sin seguir un orden. El concepto nominal sugiere su uso que es etiquetar o nombrar.

El uso de un número es para identificar. Un número no tiene mayor valor que otro. Un ejemplo son los números de las camisetas de los jugadores de un equipo de béisbol. El número mayor no significa que tiene el mayor atributo que el número menor, es aleatorio o de capricho personal a quien otorga el número.

también encontramos escala de altura,escala de perspectiva,escala de anchura,escala de profundidad Para el procesamiento de datos, los nombres pueden ser remplazados por números, pero en ese caso el valor numérico de los números dados es irrelevante.

El único tipo de comparaciones que se pueden hacer con este tipo de variables es el de igualdad o diferencia. Las comparaciones “mayor que”o “menor que” no existen entre nombres, así como tampoco operaciones tales como la adición, la substracción, etc.

Ejemplos de medidas nominales son algunas de estas variables: estado marital, género, raza, credo religioso, afiliación política, lugar de nacimiento, el número de seguro social, el sexo, los números de teléfono, entre otros.

La única medida de tendencia central que se puede hacer es la moda. La dispersión estadística se puede hacer con tasa de variación, índice de variación cualitativa, o mediante entropía de información. No existe la desviación estándar.

Medida ordinal

El nivel ordinal describe las variables a lo largo de un continuo sobre el que se pueden ordenar los valores. En este caso las variables no sólo se asignan a grupos sino que además pueden establecerse relaciones de mayor que, menor que o igual que, entre los elementos.

Por ejemplo, se puede ordenar al conjunto de alumnos del módulo de diversificación curricular en función de la calificación obtenida en el último examen.

Las variables de este tipo además de nombrar se considera el asignar un orden a los datos. Esto implica que un número de mayor cantidad tiene un más alto grado de atributo medido en comparación con un número menor, pero las diferencias entre rangos pueden no ser iguales.

Las operaciones matemáticas posibles son: contabilizar los elementos, igualdad y desigualdad, además de ser mayor o menor que.

En esta clasificación, los números asignados a los objetos representan el orden o rango de las entidades medidas. Los números se denominan ordinales, las variables se denominan ordinales o variables de rango. Se pueden hacer comparaciones como “mayor que”, “menor que”, además de las comparaciones de igualdad o diferencia.

Las operaciones aritméticas como la sustracción a la adición no tienen sentido en este tipo de variables.

Ejemplos de variables ordinales son: la dureza de los minerales, los resultados de una carrera de caballos, actitudes como preferencias, conservatismo o prejuicio, el nivel socioeconómico, orden de llegada de los corredores, entre otros.

Las medidas de tendencia central de una variable ordinal pueden representarse por su moda o su mediana. La mediana proporciona más información.

Medida de intervalo o intervalar

El nivel de intervalo procede del latín interval lun (espacio entre dos paredes). Este nivel integra las variables que pueden establecer intervalos iguales entre sus valores.

Las variables del nivel de intervalos permiten determinar la diferencia entre puntos a lo largo del mismo continuo. Las operaciones posibles son todas las de escalas anteriores, más la suma y la resta.

En este tipo de medida, los números asignados a los objetos tienen todas las características de las medidas ordinales, y además las diferencias entre medidas representan intervalos equivalentes.
Esto es, las diferencias entre una par arbitrario de medidas puede compararse de manera significativa.

Estas variables nombran, ordenan y presentan igualdad de magnitud. Por lo tanto, operaciones tales como la adición, la sustracción tienen significado.

En estas variables el punto cero de la escala es arbitrario y se pueden usar valores negativos, no significa ausencia de valor y existe una unidad de igualdad entre los valores. Las diferencias se pueden expresar como razones.

Las medidas de tendencia central pueden representarse mediante la moda, la mediana al promedio aritmético. El promedio proporciona más información.
Las variables medidas al nivel de intervalo se llaman variables de intervalo o variables de escala.

Ejemplos de este tipo de variables son la fecha, la temperatura, las puntuaciones de una prueba, la escala de actitudes, las puntuaciones de IQ, conjuntos de años, entre otros.

Medida de razón o racional

El nivel de razón, cuya denominación procede del latín ratio (cálculo), integra aquellas variables con intervalos iguales pueden situar un cero absoluto.

Estas variables nombran orden, presentan intervalos iguales y el cero significa ausencia de la característica.

El cero absoluto supone identificar una posición de ausencia total del rasgo o fenómeno. Tiene características importantes:

El valor cero no es arbitrario (no responde a las conveniencias de los investigadores). Un ejemplo claro es la temperatura. La existencia de un cero en la escala Celsius no supone la ausencia de temperatura, puesto que el cero grados centígrados está situado por arbitrio de los creadores de la escala. Por el contrario, la escala Kelvin sí tiene un cero absoluto, precisamente allí donde las moléculas cesan su actividad y no se produce por lo tanto roce entre los componentes moleculares. El cero absoluto de la escala Kelvin se sitúa a unos -273 grados centígrados.

La presencia de un cero absoluto permite utilizar operaciones matemáticas más complejas a las otras escalas. Hasta ahora se podía asignar, establecer la igualdad (nominal), mayor o menor que (ordinal), sumar y restar (intervalo) a las que se añade multiplicar, dividir, etc.

Los números asignados a los objetos tienen todas las características de las medidas de intervalo y además tienen razones significativas entre pares arbitrarios de números. Operaciones tales como la multiplicación y la división tienen significado.

La posición del cero no es arbitraria para este tipo de medida. Las variables para este nivel de medida se llaman variables racionales. La mayoría de las cantidades físicas, tales como la masa, longitud, energía, se miden en la escala racional, así como también la temperatura (en Kelvins) relativa al cero absoluto.

Las medidas de tendencia central de una variable medida a nivel racional pueden representarse por la moda, la mediana, el promedio aritmético o su promedio geométrico. Lo mismo que con la escala de intervalos, el promedio aritmético proporciona la mayor información.

Por ejemplo; el ingreso; el cero representaría que no recibe ingreso en virtud de un trabajo, la velocidad; el cero significa ausencia de movimiento. Otros ejemplos de variables racionales son la edad, y otras medidas de tiempo.

En otras palabras, la escala de razón comienza desde el cero y aumenta en números sucesivos iguales a cantidades del atributo que está siendo medido.

como también vemos las escalas de: -escala de altura -escala de anchura -escala de perspectiva -escala de profundidad

ASOCIACION ENTRE VARIABLES NOMINALES DE CORRELACION PHI

Coeficiente de contingencia

El coeficiente de contingencia C (de Karl Pearson) es una medida de relación estadística. El coeficiente de contingencia de Pearson expresa la intensidad de la relación entre dos (o más) variables nominales u ordinales. Se basa en la comparación de las frecuencias efectivamente calculadas de dos características con las frecuencias que se hubiesen esperado con independencia de estas características

El coeficiente de contingencia posee una serie de características:

* No existe relación entre las variables, por tanto diremos que estas tendrán una proporción similar.

*Se utiliza para evitar el efecto del tamaño de la muestra.

*En una tabla de dos filas por columna es recomendable realizar la corrección de Yates.

También este tipo de correlación posee una serie de propiedades que tenemos que tener en cuenta:

El coeficiente de contingencia C está comprendido entre 0 y 1.

El coeficiente C presenta el valor cero cuando la relación entre las variables es nula, pero nunca alcanza el valor 1.

El máximo dependerá del numero de filas y columnas.

El coeficiente C indica la intensidad de relación entre las variables que se estan midiendo.

El valor de C depende del número de filas y columnas de la tabla de contingencia construido para su calculo.

El coeficiente C no es comparable a otros coeficientes de correlación, valores similares indicaría diferentes grados de correlación.

El coeficiente $\chi ^2$ (coeficiente Chi-cuadrado)

El coeficiente $\chi ^2$ (también llamado contingencia cuadrática), sobre el que se basa el coeficiente de contingencia, es una medida de la "intensidad" de la relación entre las características observadas :

$\chi^2=\sum_{i=1}^k \sum_{j=1}^m \frac{(h_{i,j} -\frac{h_i. h._j}{n})^2}{\frac{h_i. h._j}{n}}$

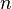El valor informativo del coeficiente $\chi ^2$ es reducido debido a que su límite superior, es decir, el valor que asume en el caso de la completa dependencia de las características observadas es dependiente de la magnitud (dimensión) de la tabla de contingencia (es decir de la cantidad de valores posibles de las variables) y del tamaño del universo estudiado $n$ . No está dada entonces la factibilidad de la comparación de valores del coeficiente $\chi^2$ sobre diferentes tablas de contingencia y tamaños muestrales.

En el caso de la completa independencia de las características, $\chi^2=0$ .

Rige que:

$0 \leq \chi^2 \leq n \cdot \min\{k-1,m-1\}$

siendo $k\,$ el número de filas y $m\,$ el número de columnas de la tabla de contingencia.

Usos

El valor de $\chi^2$ se necesita para determinar el coeficiente de contingencia C. En las pruebas de significación estadística también se utiliza el valor de $\chi^2$

Ejemplo

Sea la siguiente una tabla de contingencia proveniente de una encuesta:

	automóvil tipo sedán	automóvil tipo familiar	Totales
Obreros	19	18	37
Empleados	43	20	63
Totales	62	38	100

Cálculo del coeficiente $\chi^2$ :

$\frac{(19 -\frac{37 * 62}{100})^2}{\frac{37 * 62}{100}} + \frac{(18 -\frac{37 * 38}{100})^2}{\frac{37 * 38}{100}} + \frac{(43 -\frac{63 * 62}{100})^2}{\frac{63 * 62}{100}} + \frac{(20 -\frac{63 * 38}{100})^2}{\frac{63 * 38}{100}} = 2{,}83$

Contingencia cuadrática media

Otra medida para especificar la intensidad de la dependencia de las características en una tabla de contingencia es la contingencia cuadrática media, que en lo esencial representa una ampliación del coeficiente $\chi ^2$ :

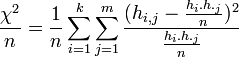
$\frac{\chi^2}{n}=\frac{1}{n} \sum_{i=1}^k \sum_{j=1}^m \frac{(h_{i,j} -\frac{h_i. h._j}{n})^2}{\frac{h_i. h._j}{n}}$

Cuanto mayor es esta medida, tanto más intensa es la relación entre las dos características

analizadas. Si ambas características (variables) son independientes, entonces cada uno de los sumandos se hace 0, a consecuencia de que se hace 0 el numerador de la fracción y con ello la medida misma también. En el caso de una tabla de contingencia de 2x2 la medida está normada y asume valores en el intervalo [0,1].

Coeficiente de contingencia de Karl Pearson

$\chi ^2$ puede asumir valores en principio muy grandes y no está limitado al intervalo $[0,1]$ . Para excluir la dependencia del coeficiente de contingencia del tamaño de la muestra, se calcula en base a 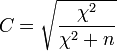$\chi ^2$ el coeficiente de contingencia C (también denominado CC o K) de Karl Pearson:

$C=\sqrt{\frac{\chi ^2}{\chi^2 + n}}$ .

donde $n$ es el tamaño de la muestra.

Este puede asumir valores en el intervalo [0,1). Resulta problemático que el límite superior del coeficiente de contingencia C sea dependiente del número de las dimensiones observadas:

Aquí rige $C\in \left[0,\sqrt{\frac{k-1}{k}} \right]$ , donde $k=\min(|I|,|J|)$ el mínimo de entre la cantidad de formas posibles de la característica en las variables estudiadas.

Coeficiente de contingencia corregido

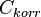Para poder excluir, además de la influencia del tamaño de la muestra, también la influencia de de la dimensión de las tablas de contingencia consideradas (el número de formas de la característica) sobre el límite superior del coeficiente y asegurar así la comparabilidad de los resultados, se utiliza con frecuencia el coeficiente de contingencia corregido $C_{korr}$ (también denominado $K^*$ ) para medir la relación:

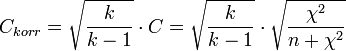$C_{korr}=\sqrt{\frac{k}{k-1}} \cdot C = \sqrt{\frac{k}{k-1}} \cdot \sqrt{\frac{\chi ^2}{n+\chi ^2}}$ ,

donde $k$ igual que más arriba.

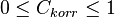Aquí rige: $0 \leq C_{korr} \leq 1$ : Un $C_{korr}\,$ cercano a 0 indica características independientes. $C_{korr}\,$ cerca de 1 señala una mayor medida de dependencia entre las características.

Para el ejemplo propuesto, resulta un coeficiente de contingencia corregido

$C_{korr} = \sqrt{\frac{2}{2-1}}*0{,}166 = 0{,}234$ .

Cramérs V

El Cramérs V (en inglés también: Cramér's V) es un coeficiente de contingencia, más precisamente, una medida de relación estadística basada en $\chi^2$ . Se denomina así en honor del matemático y estadístico sueco Harald Cramér.

El Cramérs V es una valor de medida independiente del tamaño de la muestra. Cramérs V es una medida simétrica para la intensidad de la relación entre dos o más variables de la escala nominal, cuando (por lo menos) una de las dos variables tiene por lo menos dos formas (valores posibles). En una tabla de 2x2 el Cramérs V corresponde al Coeficiente phi.

Procedimiento

$V = \sqrt{\frac{\chi^2}{n (\min[r, c]-1)}}$ .

$n$ : Total de casos (volumen de la muestra)

$min[r,c]$ es el menor entre ambos valores «número de filas» (rows)" y "número de columnas (columns)"

Interpretación

En cualquier tabla de contingencia – independientemente de la cantidad de filas y columnas – Cramérs V está entre 0 y 1. Puede usarse para tablas de contingencia de cualquier tamaño. Un Cramérs V que es mayor que 0,3 es considerado en ciencias sociales como una correlación significativa.

Rango de valores [0 hasta 1]

Cramérs V = 0: no hay relación entre X e Y
Cramérs V = 1: hay una relación perfecta entre X e Y
Cramérs V = 0,6: hay una correlación relativamente intensa entre X e Y

Dado que Cramérs V es un número siempre positivo, no se pueden hacer afirmaciones acerca de la dirección de la relación.

C

oeficiente Phi $\boldsymbol{\phi} \;$

El coeficiente Phi (también llamado coeficiente de correlación de cuatro campos) $\phi \,$ (también $\widehat{r_\phi}$ ) es una medida para la intensidad de la relación entre variables dicotómicas.

Cálculo

para estimar la correlación de cuatro campos entre dos caraterísticas dicotómicas A y B, se construye primeramente una tabla de contingencia que contiene la distribución de frecuencia conjunta de las variables.

	A=0	A=1	Total
B=0	a	b	a+b
B=1	c	d	c+d
Total	a+c	b+d	a+b+c+d

Con los datos de la tabla se puede calcular $\phi \;$ según la fórmula

$\phi= \frac{a \cdot d- b \cdot c}{\sqrt{(a+b)\cdot(c+d)\cdot(a+c)\cdot(b+d)}}$ .

Ejemplos

Medida de la asociación entre

Aprobación o rechazo de una decisión política acerca del género,
Presentación o en su defecto, no presentación de un aviso publicitario y compra o no-compra de un producto.
Aplicación de $\phi \,$ a una matriz de confusión con dos clases.

Nota

Entre $\phi \,$ y $\chi^2\,$ existe la relación $\chi^2=n \cdot \phi^2$ bzw. $\phi^2=\frac{\chi^2}{n}$ , donde $n\,$ designa al número de observaciones. Con ello $\phi\,$ es la raíz cuadrada (sin que importe el signo) de la contingencia media cuadrática (ver más arriba).

Como prueba de significación estadística, bajo el supuesto de que $\phi \,$ es igual a cero, $n \cdot \phi^2$ tiene una distribución Chi Cuadrado con un grado de libertad