Coeficiente de contingencia
El coeficiente de contingencia C (de Karl Pearson) es una medida de relación estadística. El coeficiente de contingencia de Pearson expresa la intensidad de la relación entre dos (o más) variables nominales u ordinales. Se basa en la comparación de las frecuencias efectivamente calculadas de dos características con las frecuencias que se hubiesen esperado con independencia de estas características
El coeficiente de contingencia posee una serie de características:
* No existe relación entre las variables, por tanto diremos que estas tendrán una proporción similar.
*Se utiliza para evitar el efecto del tamaño de la muestra.
*En una tabla de dos filas por columna es recomendable realizar la corrección de Yates.
También este tipo de correlación posee una serie de propiedades que tenemos que tener en cuenta:
El coeficiente de contingencia C está comprendido entre 0 y 1.
El coeficiente C presenta el valor cero cuando la relación entre las variables es nula, pero nunca alcanza el valor 1.
El máximo dependerá del numero de filas y columnas.
El coeficiente C indica la intensidad de relación entre las variables que se estan midiendo.
El valor de C depende del número de filas y columnas de la tabla de contingencia construido para su calculo.
El coeficiente C no es comparable a otros coeficientes de correlación, valores similares indicaría diferentes grados de correlación.
El coeficiente  (coeficiente Chi-cuadrado)
(coeficiente Chi-cuadrado)
 (coeficiente Chi-cuadrado)
(coeficiente Chi-cuadrado)
El coeficiente  (también llamado contingencia cuadrática), sobre el que se basa el coeficiente de contingencia, es una medida de la "intensidad" de la relación entre las características observadas :
(también llamado contingencia cuadrática), sobre el que se basa el coeficiente de contingencia, es una medida de la "intensidad" de la relación entre las características observadas :
 (también llamado contingencia cuadrática), sobre el que se basa el coeficiente de contingencia, es una medida de la "intensidad" de la relación entre las características observadas :
(también llamado contingencia cuadrática), sobre el que se basa el coeficiente de contingencia, es una medida de la "intensidad" de la relación entre las características observadas :
El valor informativo del coeficiente  es reducido debido a que su límite superior, es decir, el valor que asume en el caso de la completa dependencia de las características observadas es dependiente de la magnitud (dimensión) de la tabla de contingencia (es decir de la cantidad de valores posibles de las variables) y del tamaño del universo estudiado
es reducido debido a que su límite superior, es decir, el valor que asume en el caso de la completa dependencia de las características observadas es dependiente de la magnitud (dimensión) de la tabla de contingencia (es decir de la cantidad de valores posibles de las variables) y del tamaño del universo estudiado 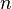 . No está dada entonces la factibilidad de la comparación de valores del coeficiente
. No está dada entonces la factibilidad de la comparación de valores del coeficiente  sobre diferentes tablas de contingencia y tamaños muestrales.
sobre diferentes tablas de contingencia y tamaños muestrales.
 es reducido debido a que su límite superior, es decir, el valor que asume en el caso de la completa dependencia de las características observadas es dependiente de la magnitud (dimensión) de la tabla de contingencia (es decir de la cantidad de valores posibles de las variables) y del tamaño del universo estudiado
es reducido debido a que su límite superior, es decir, el valor que asume en el caso de la completa dependencia de las características observadas es dependiente de la magnitud (dimensión) de la tabla de contingencia (es decir de la cantidad de valores posibles de las variables) y del tamaño del universo estudiado 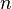 . No está dada entonces la factibilidad de la comparación de valores del coeficiente
. No está dada entonces la factibilidad de la comparación de valores del coeficiente  sobre diferentes tablas de contingencia y tamaños muestrales.
sobre diferentes tablas de contingencia y tamaños muestrales.
En el caso de la completa independencia de las características,  .
.
 .
.
Rige que:
siendo  el número de filas y
el número de filas y  el número de columnas de la tabla de contingencia.
el número de columnas de la tabla de contingencia.
 el número de filas y
el número de filas y  el número de columnas de la tabla de contingencia.
el número de columnas de la tabla de contingencia.Usos
El valor de  se necesita para determinar el coeficiente de contingencia C. En las pruebas de significación estadística también se utiliza el valor de
se necesita para determinar el coeficiente de contingencia C. En las pruebas de significación estadística también se utiliza el valor de 
 se necesita para determinar el coeficiente de contingencia C. En las pruebas de significación estadística también se utiliza el valor de
se necesita para determinar el coeficiente de contingencia C. En las pruebas de significación estadística también se utiliza el valor de 
Ejemplo
Sea la siguiente una tabla de contingencia proveniente de una encuesta:
| automóvil tipo sedán | automóvil tipo familiar | Totales | |
| Obreros | 19 | 18 | 37 |
| Empleados | 43 | 20 | 63 |
| Totales | 62 | 38 | 100 |
Cálculo del coeficiente  :
:
 :
:
Contingencia cuadrática media
Otra medida para especificar la intensidad de la dependencia de las características en una tabla de contingencia es la contingencia cuadrática media, que en lo esencial representa una ampliación del coeficiente  :
:
 :
:
Cuanto mayor es esta medida, tanto más intensa es la relación entre las dos características
analizadas. Si ambas características (variables) son independientes, entonces cada uno de los sumandos se hace 0, a consecuencia de que se hace 0 el numerador de la fracción y con ello la medida misma también. En el caso de una tabla de contingencia de 2x2 la medida está normada y asume valores en el intervalo [0,1].
Coeficiente de contingencia de Karl Pearson
 puede asumir valores en principio muy grandes y no está limitado al intervalo
puede asumir valores en principio muy grandes y no está limitado al intervalo ![[0,1]](http://upload.wikimedia.org/wikipedia/es/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) . Para excluir la dependencia del coeficiente de contingencia del tamaño de la muestra, se calcula en base a
. Para excluir la dependencia del coeficiente de contingencia del tamaño de la muestra, se calcula en base a  el coeficiente de contingencia C (también denominado CC o K) de Karl Pearson:
el coeficiente de contingencia C (también denominado CC o K) de Karl Pearson: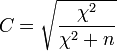 .
.
- donde
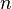 es el tamaño de la muestra.
es el tamaño de la muestra.
Este puede asumir valores en el intervalo [0,1). Resulta problemático que el límite superior del coeficiente de contingencia C sea dependiente del número de las dimensiones observadas:
Aquí rige ![C\in \left[0,\sqrt{\frac{k-1}{k}} \right]](http://upload.wikimedia.org/wikipedia/es/math/8/2/1/8216b9e69cf2ae190bcab5ee0555311a.png) , donde
, donde  el mínimo de entre la cantidad de formas posibles de la característica en las variables estudiadas.
el mínimo de entre la cantidad de formas posibles de la característica en las variables estudiadas.
![C\in \left[0,\sqrt{\frac{k-1}{k}} \right]](http://upload.wikimedia.org/wikipedia/es/math/8/2/1/8216b9e69cf2ae190bcab5ee0555311a.png) , donde
, donde  el mínimo de entre la cantidad de formas posibles de la característica en las variables estudiadas.
el mínimo de entre la cantidad de formas posibles de la característica en las variables estudiadas.Coeficiente de contingencia corregido
Para poder excluir, además de la influencia del tamaño de la muestra, también la influencia de de la dimensión de las tablas de contingencia consideradas (el número de formas de la característica) sobre el límite superior del coeficiente y asegurar así la comparabilidad de los resultados, se utiliza con frecuencia el coeficiente de contingencia corregido 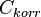 (también denominado
(también denominado  ) para medir la relación:
) para medir la relación:
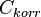 (también denominado
(también denominado  ) para medir la relación:
) para medir la relación: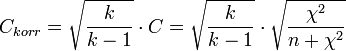 ,
,
donde  igual que más arriba.
igual que más arriba.
 igual que más arriba.
igual que más arriba.
Aquí rige: 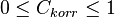 : Un
: Un  cercano a 0 indica características independientes.
cercano a 0 indica características independientes.  cerca de 1 señala una mayor medida de dependencia entre las características.
cerca de 1 señala una mayor medida de dependencia entre las características.
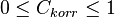 : Un
: Un  cercano a 0 indica características independientes.
cercano a 0 indica características independientes.  cerca de 1 señala una mayor medida de dependencia entre las características.
cerca de 1 señala una mayor medida de dependencia entre las características.
Para el ejemplo propuesto, resulta un coeficiente de contingencia corregido
 .
.Cramérs V
El Cramérs V (en inglés también: Cramér's V) es un coeficiente de contingencia, más precisamente, una medida de relación estadística basada en  . Se denomina así en honor del matemático y estadístico sueco Harald Cramér.
. Se denomina así en honor del matemático y estadístico sueco Harald Cramér.
 . Se denomina así en honor del matemático y estadístico sueco Harald Cramér.
. Se denomina así en honor del matemático y estadístico sueco Harald Cramér.
El Cramérs V es una valor de medida independiente del tamaño de la muestra. Cramérs V es una medida simétrica para la intensidad de la relación entre dos o más variables de la escala nominal, cuando (por lo menos) una de las dos variables tiene por lo menos dos formas (valores posibles). En una tabla de 2x2 el Cramérs V corresponde al Coeficiente phi.
Procedimiento
![V = \sqrt{\frac{\chi^2}{n (\min[r, c]-1)}}](http://upload.wikimedia.org/wikipedia/es/math/4/a/9/4a9024c9515a54a00f01dcd095b63607.png) .
.
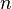 : Total de casos (volumen de la muestra)
: Total de casos (volumen de la muestra)![min[r,c]](http://upload.wikimedia.org/wikipedia/es/math/9/5/e/95ebe9653ea29b75c9bbf4eb24028ecb.png) es el menor entre ambos valores «número de filas» (rows)" y "número de columnas (columns)"
es el menor entre ambos valores «número de filas» (rows)" y "número de columnas (columns)"
Interpretación
En cualquier tabla de contingencia – independientemente de la cantidad de filas y columnas – Cramérs V está entre 0 y 1. Puede usarse para tablas de contingencia de cualquier tamaño. Un Cramérs V que es mayor que 0,3 es considerado en ciencias sociales como una correlación significativa.
- Rango de valores [0 hasta 1]
- Cramérs V = 0: no hay relación entre X e Y
- Cramérs V = 1: hay una relación perfecta entre X e Y
- Cramérs V = 0,6: hay una correlación relativamente intensa entre X e Y
Dado que Cramérs V es un número siempre positivo, no se pueden hacer afirmaciones acerca de la dirección de la relación.
C
oeficiente Phi 
El coeficiente Phi (también llamado coeficiente de correlación de cuatro campos)  (también
(también  ) es una medida para la intensidad de la relación entre variables dicotómicas.
) es una medida para la intensidad de la relación entre variables dicotómicas.
 (también
(también  ) es una medida para la intensidad de la relación entre variables dicotómicas.
) es una medida para la intensidad de la relación entre variables dicotómicas.Cálculo
para estimar la correlación de cuatro campos entre dos caraterísticas dicotómicas A y B, se construye primeramente una tabla de contingencia que contiene la distribución de frecuencia conjunta de las variables.
| A=0 | A=1 | Total | |
|---|---|---|---|
| B=0 | a | b | a+b |
| B=1 | c | d | c+d |
| Total | a+c | b+d | a+b+c+d |
Con los datos de la tabla se puede calcular  según la fórmula
según la fórmula
 según la fórmula
según la fórmula .
.Ejemplos
Medida de la asociación entre
- Aprobación o rechazo de una decisión política acerca del género,
- Presentación o en su defecto, no presentación de un aviso publicitario y compra o no-compra de un producto.
- Aplicación de
 a una matriz de confusión con dos clases.
a una matriz de confusión con dos clases.
Nota
Entre  y
y  existe la relación
existe la relación  bzw.
bzw.  , donde
, donde  designa al número de observaciones. Con ello
designa al número de observaciones. Con ello  es la raíz cuadrada (sin que importe el signo) de la contingencia media cuadrática (ver más arriba).
es la raíz cuadrada (sin que importe el signo) de la contingencia media cuadrática (ver más arriba).
 y
y  existe la relación
existe la relación  bzw.
bzw.  , donde
, donde  designa al número de observaciones. Con ello
designa al número de observaciones. Con ello  es la raíz cuadrada (sin que importe el signo) de la contingencia media cuadrática (ver más arriba).
es la raíz cuadrada (sin que importe el signo) de la contingencia media cuadrática (ver más arriba).
Como prueba de significación estadística, bajo el supuesto de que  es igual a cero,
es igual a cero,  tiene una distribución Chi Cuadrado con un grado de libertad
tiene una distribución Chi Cuadrado con un grado de libertad
 es igual a cero,
es igual a cero,  tiene una distribución Chi Cuadrado con un grado de libertad
tiene una distribución Chi Cuadrado con un grado de libertad

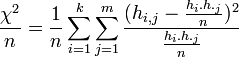
No hay comentarios:
Publicar un comentario