la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria la probabilidad de que dicho suceso ocurra. La distribución de probabilidad está definida sobre el conjunto de todos los sucesos, cada uno de los sucesos es el rango de valores de la variable aleatoria.
La distribución de probabilidad está completamente especificada por la función de distribución, cuyo valor en cada real x es la probabilidad de que la variable aleatoria sea menor o igual que x.
Definición de función de distribución
Dada una variable aleatoria 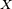 , su función de distribución,
, su función de distribución,  , es
, es
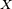 , su función de distribución,
, su función de distribución,  , es
, es
Por simplicidad, cuando no hay lugar a confusión, suele omitirse el subíndice 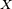 y se escribe, simplemente,
y se escribe, simplemente,  .
.
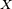 y se escribe, simplemente,
y se escribe, simplemente,  .
.
Se denomina distribución de variable discreta a aquella cuya función de probabilidad sólo toma valores positivos en un conjunto de valores de  finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
 finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:
Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde  hasta el valor
hasta el valor  .
.
 hasta el valor
hasta el valor  .
.Distribuciones de variable discreta más importantes
Las distribuciones de variable discreta más importantes son las siguientes:
- Distribución binomial
- Distribución binomial negativa
- Distribución Poisson
- Distribución geométrica
- Distribución hipergeométrica
- Distribución de Bernoulli
- Distribución Rademacher, que toma el valor 1 con probabilidad ½ y el valor -1 con probabilidad ½.
- Distribución uniforme discreta, donde todos los elementos de un conjunto finito son equiprobables.
Distribuciones de variable continua
Se denomina variable continua a aquella que puede tomar cualquiera de los infinitos valores existentes dentro de un intervalo. En el caso de variable continua la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:
una variable aleatoria o variable estocástica es una variable estadística cuyos valores se obtienen de mediciones en algún tipo de experimento aleatorio. Formalmente, una variable aleatoria es una función, que asigna eventos (p.e., los posibles resultados de tirar un dado dos veces: (1, 1), (1, 2), etc.) a números reales (p.e., su suma).
Los valores posibles de una variable aleatoria pueden representar los posibles resultados de un experimento aún no realizado, o los posibles valores de una cantidad cuyo valor actualmente existente es incierto (p.e., como resultado de medición incompleta o imprecisa). Intuitivamente, una variable aleatoria puede tomarse como una cantidad cuyo valor no es fijo pero puede tomar diferentes valores; una distribución de probabilidad se usa para describir la probabilidad de que se den los diferentes valores.
Las variables aleatorias suelen tomar valores reales, pero se pueden considerar valores aleatorios como valores lógicos, funciones... El término elemento aleatorio se utiliza para englobar todo ese tipo de conceptos relacionados. Un concepto relacionado es el de proceso estocástico, un conjunto de variables aleatorias ordenadas (habitualmente por orden o tiempo).
Definición de variable aleatoria
Informalmente una variable es aleatoria puede concebirse como un valor numérico que está afectado por el azar. Dada una variable aleatoria no es posible conocer con certeza el valor que tomará esta al ser medida o determinada, aunque si se conoce que existe una distribución de probabilidad asociada al conjunto de valores posibles.
Por ejemplo, en una epidemia de cólera, se sabe que una persona cualquiera puede enfermar o no (suceso), pero no se sabe cual de los dos sucesos va a ocurrir. Solamente se puede decir que existe una probabilidad de que la persona enferme.
Para trabajar de manera sólida con variables aleatorios en general es necesario considerar un gran número de experimentos aleatorios, para su tratamiento estadístico, cuantificar los resultados de modo que se asigne un número real a cada uno de los resultados posibles del experimento. De este modo se establece una relación funcional entre elementos del espacio muestral asociado al experimento y números reales.
Una variable aleatoria (v.a.) X es una función real definida en el espacio muestral, Ω, asociado a un experimento aleatorio.
La definición formal anterior involucra conceptos matemáticos sofisticados procedentes de la teoría de la medida, concretamente la noción de espacio de probabilidad.
Dado un espacio de probabilidad  y un espacio medible
y un espacio medible  , una aplicación
, una aplicación  es una variable aleatoria si es una aplicación
es una variable aleatoria si es una aplicación  -medible.
-medible.
 y un espacio medible
y un espacio medible  , una aplicación
, una aplicación  es una variable aleatoria si es una aplicación
es una variable aleatoria si es una aplicación  -medible.
-medible.
En la mayoría de los casos se toma como espacio medible de llegada el formado por los números reales junto con la σ-álgebra de Borel (el generado por la topología usual de  ), quedando pues la definición de esta manera:
), quedando pues la definición de esta manera:
 ), quedando pues la definición de esta manera:
), quedando pues la definición de esta manera:
Dado un espacio de probabilidad  una variable aleatoria real es cualquier función
una variable aleatoria real es cualquier función  -medible donde
-medible donde  es la σ-álgebra boreliana.
es la σ-álgebra boreliana.
 una variable aleatoria real es cualquier función
una variable aleatoria real es cualquier función  -medible donde
-medible donde  es la σ-álgebra boreliana.
es la σ-álgebra boreliana.Caracterización de variables aleatorias
Tipos de variables aleatorias
Para comprender de una manera más amplia y rigurosa los tipos de variables, es necesario conocer la definición de conjunto discreto. Un conjunto es discreto si está formado por un número finito de elementos, o si sus elementos se pueden enumerar en secuencia de modo que haya un primer elemento, un segundo elemento, un tercer elemento, y así sucesivamente.
- Variable aleatoria discreta: una v.a. es discreta si su recorrido es un conjunto discreto. La variable del ejemplo anterior es discreta. Sus probabilidades se recogen en la función de cuantía
- Variable aleatoria continua: una v.a. es continua si su recorrido no es un conjunto numerable. Intuitivamente esto significa que el conjunto de posibles valores de la variable abarca todo un intervalo de números reales. Por ejemplo, la variable que asigna la estatura a una persona extraída de una determinada población es una variable continua ya que, teóricamente, todo valor entre, pongamos por caso, 0 y 2,50 m, es posible.
- Variable aleatoria independiente: Supongamos que "X" e "Y" son variables aleatorias discretas. Si los eventos X = x / Y = y son variables aleatorias independientes. En tal caso: P(X = x, Y = y) = P( X = x) P ( Y = y).
- De manera equivalente: f(x,y) = f1(x).f2(y).
- Inversamente, si para todo "x" e "y" la función de probabilidad conjunta f(x,y) no puede expresarse sólo como el producto de una función de "x" por una función de "y" (denominadas funciones de probabilidad marginal de "X" e "Y" ), entonces "X" e "Y" son dependientes.
- Si "X" e "Y" son variables aleatorias continuas, decimos que son variables aleatorias independientes si los eventos "X ≤ x", e "Y ≤ y" y son eventos independientes para todo "x" e "y" .
- De manera equivalente: F(x,y) = F1(x).F2(y), donde F1(x) y F2(y) son las funciones de distribución (marginal) de "X" e "Y" respectivamente.
- Inversamente, "X" e "Y" son variables aleatorias dependientes si para todo "x" e "y" su función de distribución conjunta F(x,y) no puede expresarse como el producto de las funciones de distribución marginales de "X" e "Y".
- Para variables aleatorias independientes continuas, también es cierto que la función de densidad conjunta f(x,y)es el producto de las funciones densidad de probabilidad marginales de "X", f1(x), y de "Y", f2(y).
Funciones de variables aleatorias
Sea una variable aleatoria  sobre
sobre  y una función medible de Borel
y una función medible de Borel  , entonces
, entonces  será también una variable aleatoria sobre
será también una variable aleatoria sobre  , dado que la composición de funciones medibles también es medible a no ser que
, dado que la composición de funciones medibles también es medible a no ser que  sea una función medible de Lebesgue. El mismo procedimiento que permite ir de un espacio de probabilidad
sea una función medible de Lebesgue. El mismo procedimiento que permite ir de un espacio de probabilidad  a
a  puede ser utilizado para obtener la distribución de
puede ser utilizado para obtener la distribución de  . La función de probabilidad acumulada de
. La función de probabilidad acumulada de  es
es
 sobre
sobre  y una función medible de Borel
y una función medible de Borel  , entonces
, entonces  será también una variable aleatoria sobre
será también una variable aleatoria sobre  , dado que la composición de funciones medibles también es medible a no ser que
, dado que la composición de funciones medibles también es medible a no ser que  sea una función medible de Lebesgue. El mismo procedimiento que permite ir de un espacio de probabilidad
sea una función medible de Lebesgue. El mismo procedimiento que permite ir de un espacio de probabilidad  a
a  puede ser utilizado para obtener la distribución de
puede ser utilizado para obtener la distribución de  . La función de probabilidad acumulada de
. La función de probabilidad acumulada de  es
es
Si la función g es invertible, es decir g-1 existe, y es monótona creciente, entonces la anterior relación puede ser extendida para obtener
y, trabajando de nuevo bajo las mismas hipótesis de invertibilidad de g y asumiendo además diferenciabilidad, podemos hallar la relación entre las funciones de densidad de probabilidad al diferenciar ambos términos respecto de y, obteniendo
 .
.
Si g no es invertible pero cada y tiene un número finito de raíces, entonces la relación previa con la función de densidad de probabilidad puede generalizarse como
donde xi = gi-1(y). Las fórmulas de densidad no requieren que g sea creciente.
Distribución binomial
<>
<>
<>
| Distribución binomial | |
|---|---|
Función de probabilidad | |
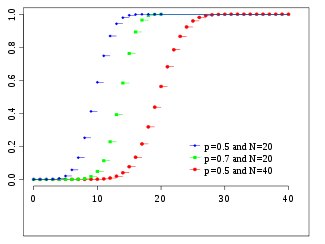 Función de distribución de probabilidad | |
 número de ensayos número de ensayos  probabilidad de éxito probabilidad de éxito | |
La distribución binomial es una distribución de probabilidad discreta que mide el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos.
Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
siendo  las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)
 las combinaciones de
las combinaciones de  en
en  (
( elementos tomados de
elementos tomados de  en
en  )
)Relaciones con otras variables aleatorias
Si 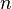 tiende a infinito y
tiende a infinito y  es tal que el producto entre ambos parámetros tiende a
es tal que el producto entre ambos parámetros tiende a  , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro
, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro 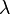 .
.
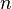 tiende a infinito y
tiende a infinito y  es tal que el producto entre ambos parámetros tiende a
es tal que el producto entre ambos parámetros tiende a  , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro
, entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro 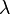 .
.
Por último, se cumple que cuando n es muy grande (usualmente se exige que  ) la distribución binomial puede aproximarse mediante la distribución normal
) la distribución binomial puede aproximarse mediante la distribución normal
 ) la distribución binomial puede aproximarse mediante la distribución normal
) la distribución binomial puede aproximarse mediante la distribución normal
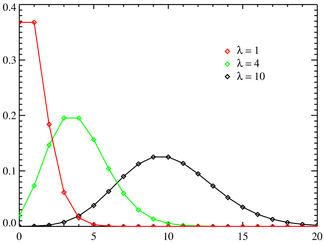
la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad que ocurra un determinado número de eventos durante cierto periodo de tiempo.
Fue descubierta por Siméon-Denis Poisson, que la dio a conocer en 1838 en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile.
Distribución normal
| Distribución normal | |
|---|---|
 La línea verde corresponde a la distribución normal estándar Función de densidad de probabilidad | |
La distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico.
Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos.
Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística es un modelo matemático que sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.








No hay comentarios:
Publicar un comentario