En estadística hay datos cualitativos y cuantitativos para las pruebas de 1, 2 y 3 o más variables. Típicos estadísticos de asociación son la regresión y la correlación, que a su vez se divide en datos cardinales y ordinales.

Ejemplos de estadísticos de asociación

Las tablas de contingencia y la matriz de correlación de tabulaciones cruzadas. Estos dos ejemplos de estadísticos miden asociaciones entre dos tablas de características con dos diferentes tratamientos y se pueden usan conjuntamente y son no parametricas, sino establecemos probabilidades.

la correlación indica la fuerza y la dirección de una relación lineal y proporcionalidad entre dos variables estadísticas. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa. La correlación entre dos variables no implica, por sí misma, ninguna relación de causalidad

Fuerza, sentido y forma de la correlación

La relación entre dos super variables cuantitativas queda representada mediante la línea de mejor ajuste, trazada a partir de la nube de puntos. Los principales componentes elementales de una línea de ajuste y, por lo tanto, de una correlación, son la fuerza, el sentido y la forma:

La fuerza extrema según el caso, mide el grado en que la línea representa a la nube de puntos: si la nube es estrecha y alargada, se representa por una línea recta, lo que indica que la relación es fuerte; si la nube de puntos tiene una tendencia elíptica o circular, la relación es débil.
El sentido mide la variación de los valores de B con respecto a A: si al crecer los valores de A lo hacen los de B, la relación lopositiva; si al crecer los valores de A disminuyen los de B, la relación es negativa.
La forma establece el tipo de línea que define el mejor ajuste: la línea recta, la curva monotónica o la curva no monotónica.

Coeficientes de correlación

Existen diversos coeficientes que miden el grado de correlación, adaptados a la naturaleza de los datos. El más conocido es el coeficiente de correlación de Pearson (introducido en realidad por Francis Galton), que se obtiene dividiendo la covarianza de dos variables por el producto de sus desviaciones estándar. Otros coeficientes son:

Coeficiente de correlación de Spearman
Correlación canónica
Coeficiente de Correlación Intraclase

Interpretación geométrica

Dados los valores muestrales de dos variables aleatorias $X (x_1, \ldots, x_n)$ e $Y (y_1, \ldots, y_n)$ , que pueden ser consideradas como vectores en un espacio a n dimensiones, puden construirse los "vectores centrados" como:

$X (x_1 - \bar x, \ldots, x_n - \bar x)$ e $Y (y_1 - \bar y, \ldots, y_n - \bar y)$ .

El coseno del ángulo alfa entre estos vectores es dada por la fórmula siguiente:

$\cos(\alpha) = \dfrac{\displaystyle \sum_{i=1}^N (x_i - \bar x)\cdot(y_i - \bar y)}{\sqrt{\displaystyle \sum_{i=1}^N (x_i - \bar x)^2}\cdot\sqrt{\displaystyle \sum_{i=1}^N (y_i - \bar y)^2}}$

Pues $\cos(\alpha)$ es el coeficiente de correlación muestral de Pearson. El coeficiente de correlación es el coseno entre ambos vectores centrados:

Si r = 1, el ángulo $\alpha = 0$ °, ambos vectores son colineales (paralelos).
Si r = 0, el ángulo $\alpha = 90$ °, ambos vectores son ortogonales.
Si r =-1, el ángulo $\alpha = 180$ °, ambos vectores son colineales de dirección opuesto.

Más generalmente: $\alpha = \arccos(r)$ .

Por supuesto, del punto vista geométrica, no hablamos de correlación lineal: el coeficiente de correlación tiene siempre un sentido, cualquiera si que sea su valor entre -1 y 1. Nos informa de modo preciso, no tanto sobre el grado de dependencia entre las variables, que sobre su distancia angular en la hiperesfera a n dimensiones.

La Iconografía de las correlaciones es un método de análisis multidimensional que reposa en esta idea. La correlacion lineal se da cuando en una nube de puntos estos se encuentran o se distribuyen alrededor de una recta.

Distribución del coeficiente de correlación

El coeficiente de correlación muestral de una muestra es de hecho una varible aleatoria, eso significa que si repetimos un experimento o consideramos diferentes muestras se obtendrán valores diferentes y por tanto el coeficiente de correlación muestral calculado a partir de ellas tendrá valores ligeramente diferentes. Para muestras grandes la variación en dicho coeficiente será menor que para muestras pequeñas. R. A. Fisher fue el primero en determinar la distribución de probabilidad para el coeficiente de correlación.

Si las dos variables aleatorias que trata de relacionarse proceden de una distribución gaussiana bivariante entonces el coeficiente de correlación r sigue una distribución de probabilidad dada por:

$f\left(r\right) = \frac{\left(n - 2\right)\, \mathbf{\Gamma}\left(n - 1\right) \left(1 - \rho^2\right)^{\frac{n - 1}{2}} \left(1 - r^2\right)^{\frac{n - 4}{2}}}{\sqrt{2\pi}\, \mathbf{\Gamma}\left(n - \frac{1}{2}\right) \left(1 - \rho r\right)^{n - \frac{3}{2}}} \,\mathbf{_2F_1}\left(\frac{1}{2}, \frac{1}{2}; \frac{2n - 1}{2}; \frac{\rho r + 1}{2}\right)$

donde:

$\mathbf{\Gamma}$ es la distribución gamma

$\,\mathbf{_2F_1}(a,b;c;z)$ es la función gaussiana hipergeométrica.

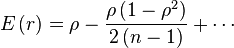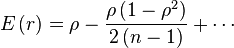Nótese que $E\left(r\right) = \rho - \frac{\rho \left(1 - \rho^2\right)}{2 \left(n - 1\right)} + \cdots$ , por tanto r es estimador sesgado de $\,\rho$ .

Puede obtenerse un estimador aproximado no sesgado resolviendo la ecuación:

$r = E\left(r\right) = \rho - \frac{\rho \left(1 - \rho^2\right)}{2 \left(n - 1\right)}$ for $\,\rho$

Aunque, la solucón:

$\breve{\rho} = r \left[1 + \frac{1 - r^2}{2\left(n - 1\right)}\right]$

es subóptima. Se puede obtener un estimador sesgado con mínima varianza para grandes valores de n, con sesgo de orden $\frac{1}{n - 1}$ buscando el máximo de la expresión:

$\log{f\left(r\right)}$ , i.e. $\hat{\rho} = r \left[1 - \frac{1 - r^2}{2\left(n - 1\right)}\right]$

En el caso especial de que $\,\rho = 0$ , la distribución original puede ser reescrita como:

$f\left(r\right) = \frac{\left(1 - r^2\right)^{\frac{n - 4}{2}}}{\mathbf{B}\left(\frac{1}{2}, \frac{n - 2}{2}\right)}$

donde $\mathbf{B}$ es la función beta

Diagrama de dispersión

Un diagrama de dispersión es un tipo de diagrama matemático que utiliza las coordenadas cartesianas para mostrar los valores de dos variables para un conjunto de datos.

Los datos se muestran como un conjunto de puntos, cada uno con el valor de una variable que determina la posición en el eje horizontal y el valor de la otra variable determinado por la posición en el eje vertical. Un diagrama de dispersión se llama también gráfico de dispersión.

Descripción

Se emplea cuando una variable está bajo el control del experimentador. Si existe un parámetro que se incrementa o disminuye de forma sistemática por el experimentador, se le denomina parámetro de control o variable independiente = eje de x y habitualmente se representa a lo largo del eje horizontal.

La variable medida o dependiente = eje de y usualmente se representa a lo largo del eje vertical. Si no existe una variable dependiente, cualquier variable se puede representar en cada eje y el diagrama de dispersión mostrará el grado de correlación (no causalidad) entre las dos variables.

Un diagrama de dispersión puede sugerir varios tipos de correlaciones entre las variables con un intervalo de confianza determinado. La correlación puede ser positiva (aumento), negativa (descenso), o nula (las variables no están correlacionadas). Se puede dibujar una línea de ajuste (llamada también "línea de tendencia") con el fin de estudiar la correlación entre las variables.

Una ecuación para la correlación entre las variables puede ser determinada por procedimientos de ajuste. Para una correlación lineal, el procedimiento de ajuste es conocido como regresión lineal y garantiza una solución correcta en un tiempo finito.

Uno de los aspectos más poderosos de un gráfico de dispersión, sin embargo, es su capacidad para mostrar las relaciones no lineales entre las variables. Además, si los datos son representados por un modelo de mezcla de relaciones simples, estas relaciones son visualmente evidentes como patrones superpuestos.

El diagrama de dispersión es una de las herramientas básicas de control de calidad, que incluyen además el histograma, el diagrama de Pareto, la hoja de verificación, los gráficos de control, el diagrama de Ishikawa y el (diagrama de flujo).

El papel de la estadistica en la investigacion

jueves, 14 de junio de 2012

MEDIDAS DE ASOCIACION