El concepto de probabilidad nace con el deseo del hombre de conocer con certeza los eventos futuros. Es por ello que el estudio de probabilidades surge como una herramienta utilizada por los nobles para ganar en los juegos y pasatiempos de la época. El desarrollo de estas herramientas fue asignado a los matemáticos de la corte.
Con el tiempo estas técnicas matemáticas se perfeccionaron y encontraron otros usos muy diferentes para la que fueron creadas. Actualmente se continúo con el estudio de nuevas metodologías que permitan maximizar el uso de la computación en el estudio de las probabilidades disminuyendo, de este modo, los márgenes de error en los cálculos.
A través de la historia se han desarrollado tres enfoques conceptuales diferentes para definir la probabilidad y determinar los valores e probabilidad:
El enfoque clásico
Dice que si hay x posibles resultados favorables a la ocurrencia de un evento A y z posibles resultados desfavorables a la ocurrencia de A, y todos los resultados son igualmente posibles y mutuamente excluyente (no pueden ocurrir los dos al mismo tiempo), entonces la probabilidad de que ocurra A es:

El enfoque clásico de la probabilidad se basa en la suposición de que cada resultado sea igualmente posible.
Este enfoque es llamado enfoque a priori porque permite, (en caso de que pueda aplicarse) calcular el valor e probabilidad antes de observar cualquier evento de muestra.
Ejemplo:
Si tenemos en una caja 15 piedras verdes y 9 piedras rojas. La probabilidad de sacar una piedra roja en un intento es:
El enfoque de frecuencia relativa
También llamado Enfoque Empírico, determina la probabilidad sobre la base de la proporción de veces que ocurre un evento favorable en un numero de observaciones. En este enfoque no ese utiliza la suposición previa de aleatoriedad. Porque la determinación de los valores de probabilidad se basa en la observación y recopilación de datos.
Ejemplo:
Se ha observado que 9 de cada 50 vehículos que pasan por una esquina no tienen cinturón de seguridad. Si un vigilante de transito se para en esa misma esquina un ida cualquiera ¿Cuál será la probabilidad de que detenga un vehículo sin cinturón de seguridad?
Tanto el enfoque clásico como el enfoque empírico conducen a valores objetivos de probabilidad, en el sentido de que los valores de probabilidad indican al largo plazo la tasa relativa de ocurrencia del evento.
El enfoque subjetivo
Dice que la probabilidad de ocurrencia de un evento es el grado de creencia por parte de un individuo de que un evento ocurra, basado en toda la evidencia a su disposición. Bajo esta premisa se puede decir que este enfoque es adecuado cuando solo hay una oportunidad de ocurrencia del evento. Es decir, que el evento ocurrirá o no ocurrirá esa sola vez. El valor de probabilidad bajo este enfoque es un juicio personal
Concepto de Probabilidad
Se define como cálculo de probabilidad al conjunto de reglas que permiten determinar si un fenómeno ha de producirse, fundando la suposición en el cálculo, las estadísticas o la teoría
El objetivo de esta práctica es realizar varios experimentos de probabilidad, anotar los resultados y posteriormente compararlos con los resultados teóricos.
Objetivos de las Probabilidades
El objetivo fundamental de la probabilidad, es la de mostrar al alumno la importancia y utilidad del Método Estadístico en el ámbito económico-empresarial. Con tal fin, el alumno deberá aprender a manejar los métodos y técnicas más adecuadas para el correcto tratamiento y análisis de la información proporcionada por los datos que genera la actividad económica.
Para ello se comienza afianzando los conocimientos que el alumno ya posee de Estadística Descriptiva, además de algunos conceptos nuevos relacionados con este tema.
El valor de la probabilidad
El valor más pequeño que puede tener la probabilidad de ocurrencia de un evento es igual a 0, el cual indica que el evento es imposible, y el valor mayor es 1, que indica que el evento ciertamente ocurrirá. Entonces si decimos que P(A) es la probabilidad de ocurrencia de un evento A y P(A´ ) la probabilidad de no-ocurrencia de A, tenemos que:
Eventos mutuamente excluyentes y eventos no excluyentes
Dos o más eventos son mutuamente excluyentes o disjuntos, si no pueden ocurrir simultáneamente. Es decir, la ocurrencia de un evento impide automáticamente la ocurrencia del otro evento (o eventos).
Ejemplo:
Al lanzar una moneda solo puede ocurrir que salga cara o sello pero no los dos a la vez, esto quiere decir que estos eventos son excluyentes.
Dos o más eventos son no excluyentes, o conjuntos, cuando es posible que ocurran ambos. Esto no indica que necesariamente deban ocurrir estos eventos en forma simultánea.
Ejemplo:
Si consideramos en un juego de domino sacar al menos un blanco y un seis, estos eventos son no excluyentes porque puede ocurrir que salga el seis blanco.
Reglas de la Adición
La Regla de la Adición expresa que: la probabilidad de ocurrencia de al menos dos sucesos A y B es igual a:
P(A o B) = P(A) U P(B) = P(A) + P(B) si A y B son mutuamente excluyente
P(A o B) = P(A) + P(B) – P(A y B) si A y B son no excluyentes
Siendo: P(A) = probabilidad de ocurrencia del evento A
P(B) = probabilidad de ocurrencia del evento B
P(A y B) = probabilidad de ocurrencia simultanea de los eventos A y B
Eventos Independientes
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.
Eventos dependientes
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que A|B no es una fracción.
P(A|B) = P(A y B)/P(B) o P(B|A) = P(A y B)/P(A)
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes
P(A y B) = P(A B) = P(A)P(B|A) si A y B son dependientes
P(A y B) = P(A B) = P(B)P(A|B) si A y B son dependientes
Distribución de probabilidad normal
Es una distribución de probabilidad continua que es tanto simétrica como mesocurtica. La curva que representa la distribución de probabilidad normal se describe generalmente como en forma de campana. Esta distribución es importante en inferencia estadística por tres razones diferentes:
- Se sabe que las medidas producidas en muchos procesos aleatorios siguen esta distribución.
- Las probabilidades normales pueden utilizarse generalmente para aproximar otras distribuciones de probabilidad, tales como las distribuciones binomial y de Poisson.
- Las distribuciones estadísticas tales como la media de la muestra y la proporción de la muestra, siguen a menudo la distribución normal, sin tener en cuenta la distribución de la población
Los valores de los parámetros de la distribución de probabilidad normal son = 0 y = 1. Cualquier conjunto de valores X normalmente distribuido pueden convertirse en valores normales estándar z por medio de la formula:
Haciendo posible el uso de la tabla de proporciones de área y hace innecesario el uso de la ecuación de la función de densidad de cualquier distribución normal dada.
PRINCIPIO FUNDAMENTAL DE CONTEO
Principio que establece que todos los posibles resultados en una situación dada se pueden encontrar multiplicando el número de formas en la que puede suceder cada evento.
Por ejemplo, si podemos viajar de San Francisco a Chicago de 3 formas y después de Chicago a Nueva York en 2 formas, entonces podemos ir de San Francisco a Nueva York en 3×2, o 6 formas.
Se les denomina técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las que a continuación se explicarán y hay que destacar que éstas nos proporcionan la información de todas las maneras posibles en que ocurre un evento determinado.
Una de las técnicas de conteo fundamentales es el principio de multiplicación, el cual se ilustra mediante el diagrama de árbol.
* Notación Factorial:
Se define por un producto continuado en forma descendente y en el cual el cero factorial es ifgual a uno. Y se representa por el símbolo n!.
Por ejemplo:
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1= 3,628,800
Las operaciones fundamentales son:
a) 4! + 2! = (4 x 3 x 2 x 1) + (2 x 1) = 24 + 2 = 26
b) 4! - 2! = (4 x 3 x 2 x 1) - (2 x 1) = 24 - 2 = 22
c) (4!) (2!) = (4 x 3 x 2 x 1) * (2 x 1) = 24 * 2 = 48
d) 4! / 2! = (4 x 3 x 2 x 1) / (2 x 1) = 24 / 2 = 12
* Diagrama de Árbol:
Los diagramas de árbol son ordenaciones empleadas para enumerar todas las posibilidades lógicas de una secuencia de eventos, donde cada evento puede ocurrir en un número finito. Proporcionan un método sistemático de enumeración objetiva de los resultados.
Para la construcción de u diagrama de árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.
En el final de cada rama parcial se constituyen a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).
PERMUTACIONES Y COMBINACIONES
Cuando trabajamos con muchos objetos, estos conceptos aparecen frecuentemente. Una permutación es un arreglo de un conjunto de  objetos en un orden definido. El número de permutaciones diferentes de estos
objetos en un orden definido. El número de permutaciones diferentes de estos  objetos es
objetos es  ; esto se vé fácilmente si pensamos que para la primera alternativa disponemos de los
; esto se vé fácilmente si pensamos que para la primera alternativa disponemos de los  elementos del conjunto, cada uno de los cuales puede complementarse con los
elementos del conjunto, cada uno de los cuales puede complementarse con los  restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto
restantes como segunda opción, y así hasta llegar a la última elección, conformando el producto
 .
.
El número de permutaciones posibles al tomar

Conviene enfatizar que también en este caso distinguimos subconjuntos que hayan sido escogidos en diferente orden. Una combinación  es una selección de
es una selección de  objetos sin importar el orden en que se escojan:
objetos sin importar el orden en que se escojan:

El factor
Si un conjunto de  elementos contiene
elementos contiene  elementos idénticos de tipo 1,
elementos idénticos de tipo 1,  de tipo 2,
de tipo 2,  ,
,  de tipo
de tipo  , puede verse que el número de permutaciones posibles será
, puede verse que el número de permutaciones posibles será

Para entender lo que son las permutaciones es necesario definir lo que es una combinación y lo que es una permutación para establecer su diferencia y de esta manera entender claramente cuando es posible utilizar una combinación y cuando utilizar una permutación al momento de querer cuantificar los elementos de algún evento.
COMBINACIÓN Y PERMUTACION.
COMBINACIÓN:
Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
PERMUTACIÓN:
Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.
Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.
Enfoque Axiomático
Enfoque formal, entrega un procedimiento para la formación de nuevas cadenas de símbolos partiendo de cadenas de símbolos dados.
- Elección de conjunto de axiomas
- Reglas de inferencia
- Definición
Una fbf A es un teorema, si existe una sucesión finita de fbfs
A1,...,An tales que:
- Cada Ai es un axioma o ha sido derivada de las fórmulas precedentes mediante la aplicación de alguna regla de inferencia
- An es la fbf A (prueba de A => |- A)
Si
existe una prueba de A entonces A es teorema y se denota |-A
Axiomas
A2 |-- (q --> (p v q)) Principio de la adición
A3 |-- ((p v q) --> (q v p)) Principio de la permutación
A4 |-- ((q --> r) --> ((p v q) --> (p v r) )) Principio de la suma
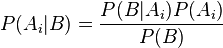
 son las probabilidades a priori.
son las probabilidades a priori. es la probabilidad de
es la probabilidad de 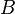 en la hipótesis
en la hipótesis  .
. son las probabilidades a posteriori.
son las probabilidades a posteriori.
En la teoría de la probabilidad el teorema de Bayes es un resultado enunciado por Thomas Bayes en 1763 que expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginal de sólo A.
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber -si se tiene algún dato más-, la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.
|
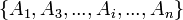 un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales
un conjunto de sucesos mutuamente excluyentes y exhaustivos, y tales que la probabilidad de cada uno de ellos es distinta de cero (0). Sea B un suceso cualquiera del que se conocen las probabilidades condicionales
No hay comentarios:
Publicar un comentario