En teoría de la probabilidad una distribución de probabilidad se llama continua si su función de distribución es continua.
Puesto que la función de distribución de una variable aleatoria X viene dada por 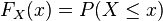 , la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo número real a, esto es, la probabilidad de que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
, la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo número real a, esto es, la probabilidad de que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
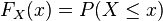 , la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo número real a, esto es, la probabilidad de que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
, la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo número real a, esto es, la probabilidad de que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
En las distribuciones de probabilidad continuas, la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:
Definición
Para una variable continua hay infinitos valores posibles de la variable y entre cada dos de ellos se pueden definir infinitos valores más. En estas condiciones no es posible deducir la probabilidad de un valor puntual de la variable; como se puede hacer en el caso de va discretas, pero es posible calcular la probabilidad acumulada hasta un cierto valor, y se puede analizar como cambia la probabilidad acumulada en cada punto, estos cambios no son probabilidades sino otro concepto: la función de densidad.
En el caso de variable continua la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:
Sea  una va continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de
una va continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de  es una función
es una función  tal que, para cualesquiera dos números
tal que, para cualesquiera dos números  y
y  siendo
siendo  .
.
 una va continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de
una va continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de  es una función
es una función  tal que, para cualesquiera dos números
tal que, para cualesquiera dos números  y
y  siendo
siendo  .
.La gráfica de
 se conoce a veces como curva de densidad, la probabilidad de que
se conoce a veces como curva de densidad, la probabilidad de que  tome un valor en el intervalo
tome un valor en el intervalo ![[a,b]](http://upload.wikimedia.org/wikipedia/es/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) es el área bajo la curva de la función de densidad; así, la función mide concentración de probabilidad alrededor de los valores de una variable aleatoria continua.
es el área bajo la curva de la función de densidad; así, la función mide concentración de probabilidad alrededor de los valores de una variable aleatoria continua. área bajo la curva de
área bajo la curva de  entre
entre  y
y 
Para que  sea una FDP (
sea una FDP ( ) sea legítima, debe satisfacer las siguientes dos condiciones:
) sea legítima, debe satisfacer las siguientes dos condiciones:
 sea una FDP (
sea una FDP ( ) sea legítima, debe satisfacer las siguientes dos condiciones:
) sea legítima, debe satisfacer las siguientes dos condiciones:- 1.

 0 para toda
0 para toda  .
.
- 2.

Ya que la probabilidad es siempre un número positivo, la FDP es una función no decreciente que cumple:
- 1.
 . Es decir, la probabilidad de todo el espacio muestral es 1.
. Es decir, la probabilidad de todo el espacio muestral es 1.
- 2.
 . Es decir, la probabilidad del suceso nulo es cero.
. Es decir, la probabilidad del suceso nulo es cero.
Algunas FDP están declaradas en rangos de
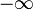 a
a  , como la de la distribución normal.
, como la de la distribución normal.
La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ = 0, y por desviación típica la unidad, σ =1.
Su función de densidad es:

Su gráfica es:

La probabilidad de la variable X dependerá del área del recinto sombreado en la figura. Y para calcularla utilizaremos una tabla.
Tipificación de la variable
Para poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).
CALCULO DEL AREA BAJO LA CURVA
APROXIMACIÓN AL ÁREA BAJO UNA CURVA
Si conocemos la ecuación de una curva
y = f(x) que toma valores no negativos, ¿cómo calcularemos el área entre la curva, el eje X y dos abscisas,
x = a y x = b?
Una idea útil consiste en dividir [a,b] en tramos y aproximar el área mediante rectángulos con
base en el eje X y altura el mínimo valor que toma la función en cada tramo.
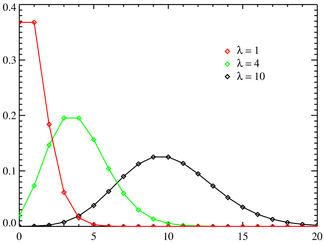
la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad que ocurra un determinado número de eventos durante cierto periodo de tiempo.
Fue descubierta por Siméon-Denis Poisson, que la dio a conocer en 1838 en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre la probabilidad de los juicios en materias criminales y civiles).
La función de masa de la distribución de Poisson es
donde
- k es el número de ocurrencias del evento o fenómeno (la función nos da la probabilidad de que el evento suceda precisamente k veces).
- λ es un parámetro positivo que representa el número de veces que se espera que ocurra el fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra k veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.e es la base de los logaritmos naturales (e = 2,71828...)
Tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a λ.
Los momentos de orden superior son polinomios de Touchard en λ cuyos coeficientes tienen una interpretación combinatorio. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el n-ésimo momento iguala al número de particiones de tamaño n.
La moda de una variable aleatoria de distribución de Poisson con un λ no entero es igual a
 , el mayor de los enteros menores que λ (los símbolos
, el mayor de los enteros menores que λ (los símbolos  representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.
representan la función parte entera). Cuando λ es un entero positivo, las modas son λ y λ − 1.La función generadora de momentos de la distribución de Poisson con valor esperado λ es
Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.
La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro λ0 a otra de parámetro λ es
La distribucion binomial o de Bernoulli
La distribución binomial está asociada a experimentos del siguiente tipo:
- Realizamos n veces cierto experimento en el que consideramos sólo la posibilidad de éxito o fracaso.
- La obtención de éxito o fracaso en cada ocasión es independiente de la obtención de éxito o fracaso en las demás ocasiones.
- La probabilidad de obtener exito o fracaso siempre es la misma en cada ocasión.





No hay comentarios:
Publicar un comentario